



Semiempirical quantum chemistry attempts to address two limitations, namely slow speed and low accuracy, of the Hartree-Fock calculation by omitting or parameterizing certain integrals based on experimental data, such as ionization energies of atoms, or dipole moments of molecules. As a result, semiempirical methods are very fast, applicable to large molecules, and may give accurate results when applied to molecules that are similar to the molecules used for parameterization. On the downside, accuracy of semiempirical methods is erratic on many systems.
Modern semiempirical models are based on the Neglect of Diatomic Differential Overlap (NDDO) method in which the overlap matrix S is replaced by the unit matrix. This allows one to replace the Hartree-Fock secular equation |H-ES| = 0 with a simpler equation |H-E|=0. The one-and two-electron integrals are evaluated approximately or parameterized based on the experimental data while three- and four-electron integrals vanish. Existing semiempirical models differ mainly by the treatment of nuclear-nuclear core repulsion and by the parameterization philosophy.
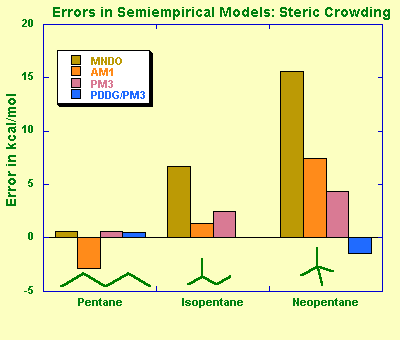
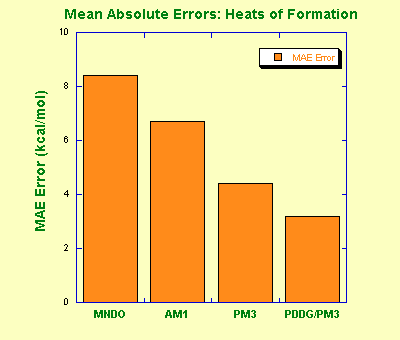
Modified Neglect of Diatomic Overlap, MNDO (by Michael Dewar and Walter Thiel, 1977) is the oldest NDDO-based model that parameterizes one-center two-electron integrals based on spectroscopic data for isolated atoms, and evaluates other two-electron integrals using the idea of multipole-multipole interactions from classical electrostatics. A classical MNDO model uses only s and p orbital basis sets while more recent MNDO/d adds d-orbitals that are especially important for the description of hypervalent sulphur species and transition metals. MNDO has a number of known deficiencies, such as inability to describe the hydrogen bond due to a strong intermolecular repulsion. The MNDO method is characterized by a generally poor reliability in predicting heats of formation. For example, highly substituted stereoisomers are predicted to be too unstable compared to linear isomers due to overestimation of repulsion is sterically crowded systems.
Austin Model 1, AM1 (by Dewar and co-workers) takes a similar approach to MNDO in approximating two-electron integrals but uses a modified expression for nuclear-nuclear core repulsion. The modified expression results in non-physical attractive forces that mimic van der Waals interactions. The modification also necessitated reparameterization of the model, which was carried out with a particular emphasis on dipole moments, ionization potentials, and geometries of molecules. While this allows for some description of the hydrogen bond, other deficiencies, such as systematic over-estimates of basicities, remained. Also, the lowest energy geometry for the water dimer is predicted incorrectly by the AM1 model. On the other hand, AM1 improves nicely some properties, such as heats of formation, over MNDO.
Parametric Method 3, PM3 (by James Stewart) uses a Hamiltonian that is very similar to the AM1 Hamiltonian but the parameterization strategy is different. While AM1 was parameterized largely based on a small number of atomic data, PM3 is parameterized to reproduce a large number of molecular properties. In some sense, chemistry gave way to statistics with the PM3 model. Different parameterization, and slightly different treatment of nuclear repulsion allow PM3 to treat hydrogen bonds rather well but it amplifies non-physical hydrogen-hydrogen attractions in other cases. This results in serious problems when analyzing intermolecular interactions (methane is predicted to be a strongly-bound dimer) or conformations of flexible molecules (OH is strongly attracted to CH3 in 1-pentanol). The accuracy of thermochemical predictions with PM3 is slightly better than that of AM1. The PM3 model has been widely used for rapid estimation of molecular properties and has been recently extended to include many elements, including some transition metals.
PDDG/PM3 (by William Jorgensen and co-workers) overcomes some of the deficiencies of the earlier NDDO based methods by using a functional group-specific modification of the core repulsion function. The Pairwize Distance Directed Gaussian (PDDG) modification provides good description of the van der Waals attraction between atoms, and the PDDG/PM3 model appears to be suitable for calculations of intermolecular complexes. Furthermore, careful reparameterization has made the PDDG/PM3 model very accurate for estimation of heats of formation. However, some limitations common to NDDO methods remain in the PDDG/PM3 model: the conformational energies are unreliable, most activation barriers are significantly overestimated, and description of radicals is erratic. So far, only C, N, O, H, S, P, Si, and halogens have been parameterized for PDDG/PM3.
The semiempirical models MNDO, AM1, and PM3 are available in many computational chemistry programs while the more recent PDDG/PM3 model has been implemented in the program BOSS. Some freely available computational chemistry programs that include many semiempirical models are MOPAC 6, MOPAC 7, and WinMopac, and ArgusLab .
Despite their limitations, semiempirical methods are often used in computational chemistry because they allow study of systems that are out of reach of more accurate methods. For example, modern semiempirical programs allow study of molecules consisting of thousands of atoms while ab initio calculations that produce similar thermochemical accuracy are feasible on molecules consisting of less than 50-70 atoms. Semiempirical calculations can be useful in many situations, such as
The limitations of semiempirical methods should be kept in mind when deciding if these are suitable tools for the task. For large systems, either molecular mechanics and semiempirical quantum mechanics could be used for optimization and calculation of conformational energies. The molecular mechanics approach is faster and in most cases produces more accurate conformational energies and geometries. Some molecular mechanics methods, such as MM3 and MM4, can also predict thermochemistry of stable species reasonably well. On the other hand, if there is no suitable force field for the system (e.g. in case of reactive intermediates or transition states), semiempirical methods may be the only choice. For small system, the compromise must be made between the semiempirical approach and the more reliable but much more time-consuming ab initio calculations. In general, semiempirical results can be trusted only in situations when they are known to work well (e.g. systems similar to molecules in the parameterization set) and strong caution should be exercised in cases where semiempirical methods are known to fail (e.g. prediction of activation barriers). Finally. it is not correct to assume that just because semiempirical methods can be used to model many larger systems, they should be used. No computational insight may be better than a wrong computational insight!

