



We saw that an approximate molecular orbital can be obtained by forming a linear combination of several atomic orbitals. One can evaluate the energy of any guess wave function as:
 The variational principle states that the energy of any guess wavefunction must be larger than or equal to the true energy calculated with the accurate wave function; the closer the guess to the true wave function, the lower the energy based on the guess wave function. The guess wave function that produces the lowest energy is thus the best approximation to the true wave function. This provides a recipe for funding the best approximate solution:
The variational principle states that the energy of any guess wavefunction must be larger than or equal to the true energy calculated with the accurate wave function; the closer the guess to the true wave function, the lower the energy based on the guess wave function. The guess wave function that produces the lowest energy is thus the best approximation to the true wave function. This provides a recipe for funding the best approximate solution:
This minimization problem is much more challenging than the minimization of molecular mechanics energy for two reasons. First, the energy of the guess wave function in the LCAO approach is given by a ratio of integrals
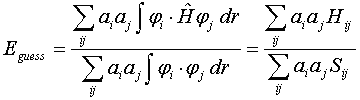
where Hij and Sij are called the resonance and overlap integrals, respectively involving different atomic orbitals. Calculation of these integrals can be challenging. Second, the minimization of Eguess with respect to coefficients ai and aj is a multi-variable minimization problem that often involves a very large number of coefficients. Thus, an efficient multi-variable minimization algorithm must be used to obtain the wavefunction that provides the lowest electronic energy for a given fixed nuclear configuration. In a common Hartree-Fock method, each molecular orbital is optimized in the presence of an average field from other electrons using the iterative algorithm outlined above. At each step, the choice of better values of coefficients ai and aj involves finding the solution to the Secular equation |H-ES| = 0.
Variational principle is commonly used to determine MO coefficients in molecular quantum mechanical calculations. Variational principle can also be used to optimize numeric parameters in wavefunctions of atoms. We saw earlier that the analytic solution for the non-relativistic hydrogen atom yielded an exponential function in the form e-ξr. Suppose that we are interested in determining the value of ξ for the ground state of a hydrogen-like atom. The best value of ξ is the one that will minimize the energy. Determination of the best value of ξ in the hydrogen atom via the variational principle is illustrated in Mathematica notebook H_Atom_Vari_Slater_AU (also available as PDF).
Notice that in the previous, almost trivial example, we already knew the mathematical form of the wavefunction (Slater, or exponential function) and just needed to optimize one parameter. In practical calculations, one usually uses a linear combination of Gaussian functions to represent a Slater function. In application to atoms, one would sometimes optimize both the Gaussian width parameters (these are customarily called "exponents", and the multiplicative coefficients to obtain an approximate wave function that closely resembles a Slater function. Optimization of Gaussian exponents for a linear combination of two Gaussian functions is illustrated in Mathematica notebook H_Atom_Vari_2GaussiansEvar_AU (also available as PDF). Such calculations are commonly used for the development of Gaussian basis sets for atoms.
Variational principle is not restricted to linear combination of similar functions, In fact, Gaussian functions are far from optimal for the description of electron density in atoms. With an insightful choice of the form of the wave function, one can use variational principle to obtain essentially accurate energies of multi-electron atoms. The best-studied system in this regard is the helium atom, for which the Hamiltonian can be separated in elliptic coordinate system. The form of the true wave function for He atom is still elusive, but one can start with the Slater function and then add terms that are thought to be appropriate for description the distribution of electron whose positions are correlation. Optimization of the exponent ξ in the Slater function for the helium atom is illustrated in Mathematica notebook Helium_Elliptic_Slater (also available as PDF). Such calculations have yielded an essentially accurate description for the helium atom.

