

In quantum mechanics, a system is characterized by its wavefunction Ψ. The properties of the system are obtained by acting on the wavefunction with a property-specific operator. For example, the energy of a molecule can be obtained by solving the equation in which the Hamiltonian operator acts on the wavefunction. Such an equation is known as the Schröedinger equation:
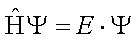
For many systems, including multi-electron atoms and molecules, the Schrödinger equation is difficult to solve because we do not know beforehand what the wavefunction of a complex system such as a molecule looks like. On the other hand, we do know how to write down the Hamiltonian operator for nearly any conceivable system. The Hamiltonian is a sum of the kinetic energy operator and the potential energy operator.
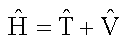
The potential energy operator corresponds to the classical interaction energies between particles in the system. In quantum mechanics, the kinetic energy operator involves a Laplacian, or the sum of unmixed second derivatives of the function with respect to the displacements. In the case of a one-variable function, the Laplacian is simply the second derivative of the function with respect to the displacement; the Laplacian and Hessian are identical when the motion is confined to one dimension. Thus, the Schröedinger equation is a second order differential equation. For example, the Schröedinger equation for a system that undergoes one-dimensional harmonic oscillations in quadratic potential around the equilibrium value can be written as:
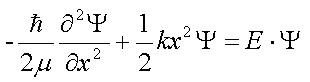
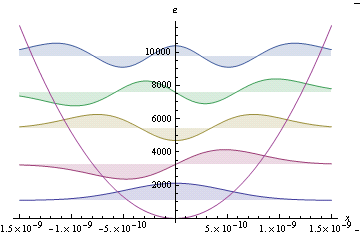
There are many possible solutions to the Schrodinger equation of a bound system. Each solution corresponds to a different energy state of the system. The discrete spectrum of solutions implies that only states with certain energy values are allowed. If the Hamiltonian is simple enough, the Schrodinger equation can be solved analytically. For example, the Schrodinger equation for the harmonic oscillator is analytically solvable; some of the wave functions and allowed energy levels are shown on the right. The harmonic oscillator is a good model for the analysis of vibrations of diatomic molecules. For example, we can see that the ground vibrational state has a certain non-zero energy, called the zero point vibrational energy. The ground state wave function is a gaussian function, and the most likely internuclear distance corresponds to no displacement from the equilibrium position. We also see that the spacing of energy levels is constant, and given by h ν for harmonic oscillator. Another exactly solvable problem is the hydrogen atom. Determination of the best value of ξ in the hydrogen atom via the variational principle in atomic units is illustrated in Mathematica notebook H_Atom_Vari_Slater_AU (also available as PDF). The accuracy of this solution can be appreciated by comparing the calculated and observed line spectra of the hydrogen atom. This requires solution in SI units and outlined in the Mathematica notebook H_Atom_Vari_Slater_AU (also available as PDF). For more complicated systems, only approximate solutions are possible.
The Hamiltonian that describes real molecules is so complex that an analytical solution to the molecular Schrodinger equation is not possible. Numerical solutions, however, are possible after making a few simplifying assumptions. Some of the most important assumptions that are almost always invoked in molecular quantum mechanics are:
The problem of coupled nuclear-electron is simplified considerably by realizing that nuclei are much heavier than electrons and one can separate the nuclear motion (e.g. the vibrational Hamiltonian) from the motion of electrons. In the Born-Oppenheimer approximation, we are interested in the electronic wavefunction at a fixed nuclear geometry. The molecular energy is now the sum of the pure electronic energy and the nuclear repulsion energy. The pure electronic energy is the energy of electrons in the field created by fixed nuclei and other electrons. We can easily calculate the nuclear repulsion energy based on fixed nuclear coordinates and the Coulomb law, but we generally cannot calculate the pure electronic energy analytically except in few trivial cases including the hydrogen molecular cation. This is considered a very valuable approximation as it allows one to think in terms of molecular structures as defined by nuclear geometry.
The wave function that describes a collection of electrons can be approximated as the linear combination of configuration determinants. In the most common approximation, only one configuration determinant, called the Slater determinant is used. The elements of the Slater determinant are individual one-electron functions called the molecular orbitals. In the Hartree-Fock method, molecular energy is evaluated from a single Slater determinant; this determinant is made of functions that depend on the average electric field due to all other electrons. Such single-determinant methods ignore some correlation in the motion of electrons.
Each one-electron molecular wave function (molecular orbital) is constructed as a Linear Combination of Atomic Orbitals. The practical reason behind LCAO is that we have a fairly good idea what atomic orbitals look like. For practical reasons, we can only include a small number of atomic orbitals. For example, most calculations involve s, p, and d atomic orbitals but better accuracy can be achieved when f and higher functions are included. Because we do not know a priory what kind of AOs are needed, and because we cannot add all possible atomic orbitals, LCAO provides an approximation to a molecular orbital. The ability to form a linear combination from different-shaped atom-centered functions allows one to approximate a molecular orbital. The LCAO coefficients determine what fraction of each atomic orbital contributes to a given molecular orbital; we can change these coefficients in an attempt to obtain a better approximation to the molecular orbital.
Each atomic orbital is approximated by Slater or Gaussian functions. The Slater functions closely mimic the behavior of wave functions of the hydrogen atom and are generally more accurate in the description of molecules via LCAO. However, the Slater functions are computationally inefficient. Gaussian functions are computationally efficient but one needs several Gaussian functions to get a Slater-like function.
